素因数分解のやり方は？【自動計算ツールもあるよ！】

素因数分解(ツールとやり方)01

中学数学の基本である素因数分解をしましょう！
フォームに正の整数を入力して「計算する」をタップしてください。下の欄に計算結果（分解された素数の一覧）が表示されます。

整数：

▼素因数▼

※最大で20桁までの入力を想定しています

ぼく(なごやっくす)

素因数分解とは、簡単にいうと「正の整数を素数のかけ算で表すこと」です。このページでは、素因数分解のやり方やコツを、画像も使って分かりやすく説明していきます！

目次(もくじ)

素因数分解のやり方【例題】

素因数分解のやり方は、以下の5ステップに分けることができます。

ぼく(なごやっくす)

実際の解き方を「180」を例題に解説していきますので、ノートを取りながら一緒にやってみましょう！

まずは、素因数分解する数を書きます。
その下に、割り算の筆算をひっくり返したような記号も一緒に書きましょう。

素因数分解のやり方01(素因数分解する整数と記号を書く)02

今回は「180」を素因数分解するので、上のようになりますね。

次に、素因数分解する数を素数で割ります。
決まりはありませんが、小さい素数から順番に割っていく（＝小さい数から順番に割れるか試していく）のがオススメです。

素因数分解のやり方02(素因数分解する数を素数で割る)02

今回の「180」は、一番小さい素数「2」で割ることができるので、上のようになりますね。

ぼく(なごやっくす)

素数は小さい順に「2,3,5,7,11,13,17,19,23,29,31…」と続きます。100までだと全部で25個の素数がありますよ。とはいえ、大きい素数については基本的に覚える必要はありません(笑)

次に、割り算した答えを素因数分解したい数（割られる数）の下に書きます。

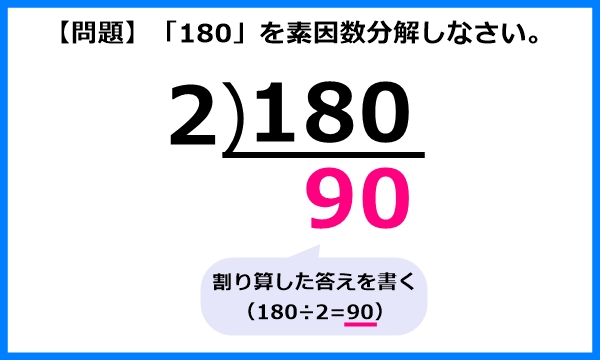
素因数分解のやり方03(割り算した答えを書く)01

今回は「180÷2=90」なので、「90」を上のように書きます。

ここまでの流れをふまえて、割り算の答えが素数になるまで繰り返します。
先ほどの「90」は、まだまだ素数で割ることができそうです。

素因数分解のやり方04(割り算の答えが素数になるまで繰り返す)02

割り算を繰り返した結果、上のようになりました。もう少しです。頑張ろう！

最後に、ここまで出てきた素数を、かけ算の形に直します。ノートに書いた数字のうち、左側と一番下の数字が素数になっているはずです。
同じ素数は指数を使ってまとめましょう。

素因数分解のやり方05(出てきた素数をかけ算の形に直す)01

「180=2×2×3×3×5」ですので、答え方は上のようになります。これでカンペキですね！

ぼく(なごやっくす)

数学のテストでは、一番下の数字を書き忘れて×(バツ)になってしまう人が結構います（僕もやらかした経験があります）。しっかり見直ししましょう！

ある数が「2の倍数」「3の倍数」「5の倍数」「11の倍数」かどうかを見分ける方法を覚えておくと、大きい数を素因数分解するときにメチャメチャ役立ちます。具体的には以下のとおりです。

倍数	法則
2の倍数	一の位が偶数（例:98、374）
3の倍数	各ケタの数の和が3の倍数になる (例:117⇒1+1+7=9)
5の倍数	一の位が0か5（例:60、9005）
11の倍数	一の位から左に向かって引き算と足し算を交互にしたとき、答えが11の倍数か0になる (例:1265⇒5-6+2-1=0)